2023年 山口大学医学部 数学 徹底分析

「山口大学医学部医学科の過去問解いたけど，数学はどのくらいできればいいの？大問別に詳しく知りたい．」

「2023年度の数学を初見で解くにはどう考えれば良い？」

「塾講師はどのような目線で問題を解いているの？」

 

そんなあなたへ向けて，「医学部・旧帝大専門塾しりうす」の塾長が徹底的に解説します！

→塾長のプロフィールはこちら

 

本記事の概要 [総評] 2023年度数学の具体的な得点戦略 (合格点から逆算) [各問解説] 2023年度数学の各大問を初見で解くには

 

[総評] 山口大学医学部医学科 2023年度数学の具体的な得点戦略 (合格点から逆算)

 

目標点は「合格者平均点」としよう

入試は大学に合格するために受けるものですから，得点戦略を練るには合格点から逆算するのが1番です．

山口大学は毎年，科目別の合格者最低点，合格者平均点，合格者最高点を公表しており，2023年度の数学(理系β)は次の表のようになっています．

合格者最高点	合格者最低点	合格者平均点
188点 (得点率：94%)	73点 (得点率：36.5%)	125.6点 (得点率：62.8%)

※山口大学医学部医学科と理学部数理科学科は「数学(理系β)」を受験することになっており，試験時間は大問4つで150分，200点満点となっています．

 

以前の記事で，科目別の目標点は，合格者最低点ではなく，合格者平均点とすることをお勧めしました．2023年度の数学(理系β)の場合，合格者平均点は125.6点(得点率 62.8%)．

各小問の配点(非公表)にもよりますが，単純計算で大問4つを計6割強解き切れれば良いわけですから，2023年度は，1完3半すれば良いと考えられるでしょう．次の大問別の目標点では，これを踏まえて解説していきます．

ちなみに，昨年度(2022年度)の数学(理系β)の合格者平均点が131.8点 (得点率：65.9%)，過去3年間の合格者平均点の平均値が131.5点 (得点率：65.7%)であったことを踏まえると，2023年度の数学は，例年よりやや難しかったことが伺えます．

実際，大問1と2にやや難しい部分がありました．どのように難しくて，初見ならそれをどのように解けば良いか，後ほど詳しく解説します．

 

大問別の難易度と目標点

2023年度の数学(理系β)では1完3半できれば合格者平均点に到達するのでした．これを踏まえると，各小問ごとの目標点は概ね次の表のようになると思います．

大問	難易度(小問別)※1	目標点に応じた大問別点数
		総合：合格平均点 126点 (63%)
[1] 場合の数	(1) A+ (2) C (3) B (4) A	25/50※2
[2] 図形	(1) A (2) B  (3) B	15/50※2
[3] 領域	(1) A (2) A (3) A (4) A	50/50
[4] 微分(III)	(1) A (2) A (3) B (4) A	35/50※2

※1 各小問の難易度は，筆者が自身の解法体系と合格者平均点に基づいて，受験者が本番で感じるであろうものを推定しています．それぞれ「A+：数行で終わる典型(易)，A：やや易  B：標準 C：やや難 D：難」を意味します．

※2 山口大学は各小問ごとの配点を公表していません．小問ごとの目標点数は，各小問の難易度から推定される配点と合格者平均点から逆算して独自に算出しています．本番の入試は受験者の出来具合などによって傾斜配点になっている可能性もあるため，この目標点はあくまで目安であることに注意してください．

 

全体戦略

全体の戦略としては，[3]で完答をし，[4]で確実に取り切って，場合の数と図形の得意な方で得点できれば合格者平均点に到達するでしょう．

そのためには，A+とAを確実に解き切って，得意な分野でBを正解することが目標になるでしょう．

実は，これは，山口大学医学部だけでなく，他の大学でも共通して言えることです．

「皆が解ける問題をいかに速く正確に解き，きちんと正解するかが合否を分ける」

と言っても過言ではないのです．

 

[各問解説] 2023年度数学の各大問を初見で解くには

続いて，各大問の解説をしていきたいと思います．

多くの解説は，「問題の正解がどうして正しいのか」を中心に説明しますが，それでは「解答の正しさ」は納得できたとしても，「解答を自力でたどり着くにはどうすれば良いか」はよくわからないということになりかねません．

しかし，入試では自力で解答が書けて初めて得点となるわけですから，解答が正しいことだけでなく，「実践的にはどうするのか」を深く理解し，習得する必要があります．

そこでしりうすでは，

• 初見で問題を見た時，どのような思考回路を取って，「答案の1行目」に至るのか
• たくさんの解法をどのように整理し，問題に応じてどのように選択するのか

を徹底的に深掘りし，どんな目新しい問題に対しても実行可能な思考法を重視して指導しています．

したがって，ここでも「答案の1行目」に至るまでの思考プロセスのみに絞って解説していきます．

ただし，全ての大問について解説しようとすると，長くなってしまうので，本記事では，やや難しいところがあった[1]と[2]のみを解説し，残りの[3]と[4]は講評に留めたいと思います．

なお，以下で述べる定石や鉄則は，すべて，授業で実際に使うオリジナルテキストに体系的に収録されているものです．

一部のみの公開となりますが，授業の雰囲気に少しでもご興味がある場合は，読んでみてくれると嬉しいです．

 

 

[1] 場合の数

「隣り合う/隣り合わない問題」と「辞書式配列」がテーマの問題でした．

一見すると典型題のように見えますが，少し注意する必要があります．順番に解説していきたいと思います．

 

(1) A+

これは「同じものを含む順列の公式」を使うだけなので割愛します．

 

(2) C　

難易度判定が高く，驚かれた方もいるかもしれません．

しかし，この問題が初見の人なら，この判定が妥当なのではないかと筆者(塾長)は考えています．

なぜなら，本問は，「隣り合う/隣り合わない問題」で定番の定石

だけでは解くことができないからです．

しかし，参考書や問題集で明示的に書かれているのはこの定石のみであることが多いため，必然的に多くの受験生が以下に述べることを全て自力で考え出さなければならない状況に陥ったことが想定されます．

その場合，たとえ方針が合っていたとしても，場合分けのミスなどが生じてしまうリスクがあり，自力で正解するのはなかなか難しかったのではないかと思います．

逆に，以下に述べることを体系化して知っている人にとっては，本問は難しくありません．

入試数学に真に有効な対策をしてきたかどうかが如実に結果に現れる問題だと思います．

 

では，どんな対策をしていたら，この問題が初見でスムーズに解けるようになるのでしょうか？それは，

• 場合分けの2系統をしっかり理解すること
• 上記に基づいて，「隣り合う/隣り合わない問題」を「同種が隣り合う」「隣り合わないものが複数ある」パターンまでしっかり理解し，解けるようになっておくこと

です．

 

場合分けの2系統

まず，「場合分けの2系統」とは，次の定石を意味します．

ここでは「常に余事象と両にらみ」であることが最も大切です．

つまり，どんな問題であっても最初に「余事象はどうかな？」と考えることが重要だということです．

これを「隣り合う/隣り合わない問題」に応用すれば，必然的に

と言うことができるでしょう．

本問(2)を例に挙げれば，「『AとDが隣り合う場合』と『AとDが隣り合わない場合』のどちらが簡単に求められるだろうか？」と最初に立ち止まって考えることが大切なのです．

逆に言えば，「『隣り合う』だから，隣り合うものをまとめればいい！」と短絡的に解法を決めてしまうと，迷宮入りする可能性があるので注意しましょう．

 

余事象の吟味 (同種の隣り合うもの)

では，(2)において，『AとDが隣り合う場合』と『AとDが隣り合わない場合』のどちらが簡単なのでしょうか？

結論から述べると，『AとDが隣り合わない場合』，つまり余事象の方が簡単です．

少し具体的に考えればなぜそうなのか自力でわかるかもしれませんが，筆者が本問を初見で解いた時は，次の例題を想起して上記の結論に達しました．

以下にオリジナルテキストに掲載している文章の一部をそのまま貼り付けます．

いかがでしょうか？

この例題1-1のように，同種の「隣り合うもの」が複数ある場合は，「まとめる」（かたまりと見る）だけでは難しいことが多く，余事象の利用，すなわち「隣り合わないもの」を全体の場合の数から引くと見通しが良くなることが多いのです．

本問も，隣り合うAとDは，「A, A, A, D」の中から選ばなければならないため，同種の「隣り合うもの」が複数あります．したがって，「AとD」が隣り合わない場合(余事象)を考える方が得策と言えます．

 

場合分け

本問がこれだけで解ける問題だったなら，(2)難易度は高くてもBと判定していたと思います．しかし，本問はこれで終わりではありません．

初見の際，筆者は，さらに次のように場合分けしました．

1. [AAA], Dを「Y,M,I」の順列の間に入れる
2. [AA], A, Dを「Y,M,I」の順列の間に入れる
3. A, A, A, Dを「Y,M,I」の順列の間に入れる

この場合分けを確実に実行するには

• 「Aは隣り合っても良い」ということを見逃さない
• 互いに排反な場合分けには何があるか？

の2点をおさえる必要があります．

これらは，いずれもその場で「思いつく」ものではなく，事前に「知識として持っておく」ものです．

しりうすではテキストや授業でしっかり扱っています．

 

(3) B

(3)も「隣り合う/隣り合わない」の定番定石だけでは解ききれない難しさはありますが，先ほどの定石(次図)を知っていれば，(2)のようにさらなる場合分けを必要としない点で，(2)よりは易しいと言えるでしょう．

この定石を本問(3)に活かすには，やはり余事象を利用して，3つのAが隣合わない場合を全体の場合の数から引けば良いです．本番でもこの方法で解いた受験生が多かったのではないでしょうか．

筆者も初見で解いたときは，最初はこの方法で手堅くいこうと考えましたが，これだけでは合っているか不安だったので，次の定石を用いて検算しました．

検算を考える際，筆者が実際に辿った思考プロセスを詳しく述べると次のようになります．

1. 「隣り合う」の定番定石を考えて，2つのAを1組の[AA]にしたい．
2. 「Aは2つではなく, 3つある」
3. 上記の定石を思い出して，[AA]と2つのAを1組にまとめた場合，「AAAを[AA]AとA[AA]と2パターンに分けて数えるとダブルカウントが発生する」ことに注意する．
4. 「[AA]とした場合の数」から「[AAA]の場合の数」を引く
5. 6!-5!=600通り

結果的にはこの方法の方が本解より速いですが，ダブルカウントを見逃してしまわないように注意が必要となります．

逆に言えば，この「少なくとも1つ隣り合う」パターンをしっかり知識として持っておくと，本問のような問題で誤りを防止できるのです．

しりうすでは，そのことも考慮して，本問題の類題を授業で扱うようにしています．

 

(4) A

これは辞書式配列の典型題であり，その定石に従って解けば良いので解説は省略します．

ただし，他の3つとは独立した小問であるため，(2)(3)が解けなかったとしても，(1)(4)だけ解くということができたことには注意が必要です．

(2)で詰まった結果，後続の小問に目を通さなかったということがあったなら，それはあまりに勿体無いので，次からは必ず全ての小問に目を通すようにしましょう．

 

[1]まとめ

以上が大問1でした．

一見，「その場で思いつけるかどうかの勝負」と考えがちな問題ですが，実は事前に体系的に知識を整理できているかどうかが問われている問題でした．

ぜひ，知識の体系化を徹底するようにしてください．

「どうやって体系化するのが最も深くかつ効率的なの？」と思った方は，ぜひしりうすにお越しください！

 

続いて，[2]に入っていきます．

 

[2] 図形

山口大学は，本問の出題意図を次のように述べています．

「三角関数の基本的な性質を理解し，平面図形の計量の問題に応用することができるか．」

まさにそうだったのです(笑)．もう少し簡単に言い換えると，本問は「角度を変数として使おう」と考えられるかどうかが最初の分岐点です．

「図形問題では，長さだけでなく角度を変数にとることもある」と言うのは簡単ですが，「どのような場合に角度を変数にとるのか」ということまで理解しなければ，本番でなかなか実行することは難しいでしょう．

ここでは，しりうすで実施する解説の一部を少し公開して，このあたりのことを中心に解説します．

 

(1) A

図形問題には，次の4通りのアプローチあります．

1. 初等幾何
2. ベクトル
3. 座標
4. 複素数平面

この4通りの特徴や使い分けの詳細についてはここでは割愛しますが，１つ言えるのは

ということです．本問は内接円の半径を求める問題ですが，これも例外ではなく，まずは初等幾何的に考えるようにします．その場合，次の定石を使うのが定番と言えるでしょう．

もう少し具体的には，三角形の面積を2通りで表します．高校数学で「三角形の面積」と言われたら，次の7つがすぐに浮かぶようにすると良いですが，公式(5)以外は，成り立ちをきちんと理解すれば「覚える」必要はないはずです．公式(5)は，導出の方針は難しくないのですが，その過程がやや面倒なので，時短のために記憶に留めておくことをお勧めしています．

本問では，内接円の半径が出てくるため公式(3)を，三角形の3辺の長さがわかっているため公式(5)を使います．

 

(2) B

(2)からが本番です．最初に次の図を描くでしょう．

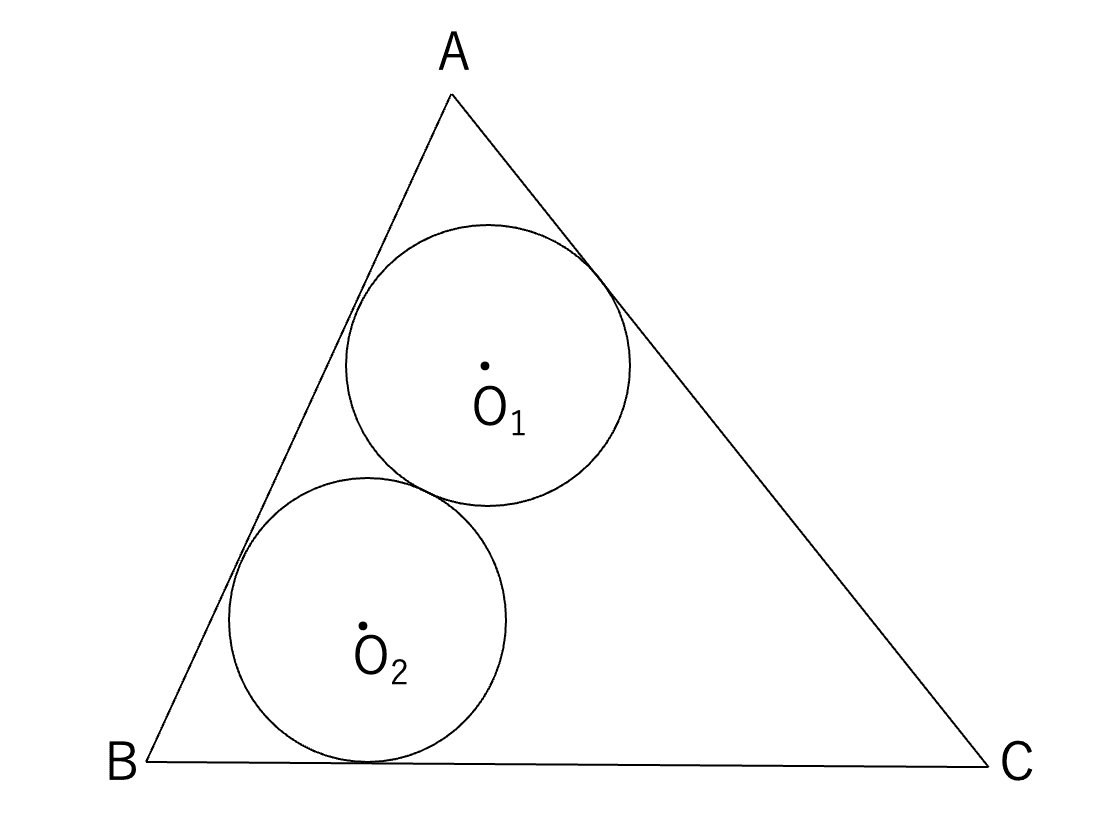
そして，図形問題ですから，

を実行します．

この図では，円が2つも出てきていますから，次の定石にしたがって補助線を描くことになると思います．

そうすると，図は次のようになります．

たとえ円に対する補助線の引き方を上の定石のように明確に言語化できていなかったとしても，類題を解いた経験から，この補助線を引くことができた受験生は多かったと思います．

しかし，問題はここからです．

円の半径をrとおけば，この補助線を引いたことにより，PQ=2rであることはわかりますが，それ以上のことがすぐには見えてきません．どうすれば良いでしょうか？

 

直角の利用

実は，初等幾何の段階において一瞬でも詰まった場合，考えてほしいのが次の定石です．

「なぜこの3つなのか」など，詳細は長くなるので割愛しますが，ここで特に忘れがちなのが「直角の利用」です．

「直角」という情報は，実は少なくとも7通りの利用法があり，その利用法を順番に吟味していくだけで突破口が見えてくることがあります．その中でも「三角比の利用」は使える場合は非常に強力です．

そして，三角比を利用する際に出てくるもの，それが「角度」です．

つまり，ここで「角度を使おう」と考えるに至るには，細かく分けると

1. まずは初等幾何
2. 円の補助線の引き方に従い，補助線を引く→直角が複数出てくる
3. 「直角の利用」を考える
4. まずは三角比
5. 角度をおいてみる

の5つのステップを頭の中で踏んでいることになります．慣れている人だとここまでで1分もかからないでしょうが，この思考が習慣化していない人は行き当たりばったりの議論をせざるを得なくなり，角度を変数としてとれるかどうかが「ひらめき」や運次第となります．

これが「解法体系」を持っているか否かの違いです．

 

この後の方針

「角度」を変数として設定してみようと思うことができたら，自ずと下図のように角度θとφを置くことになります．

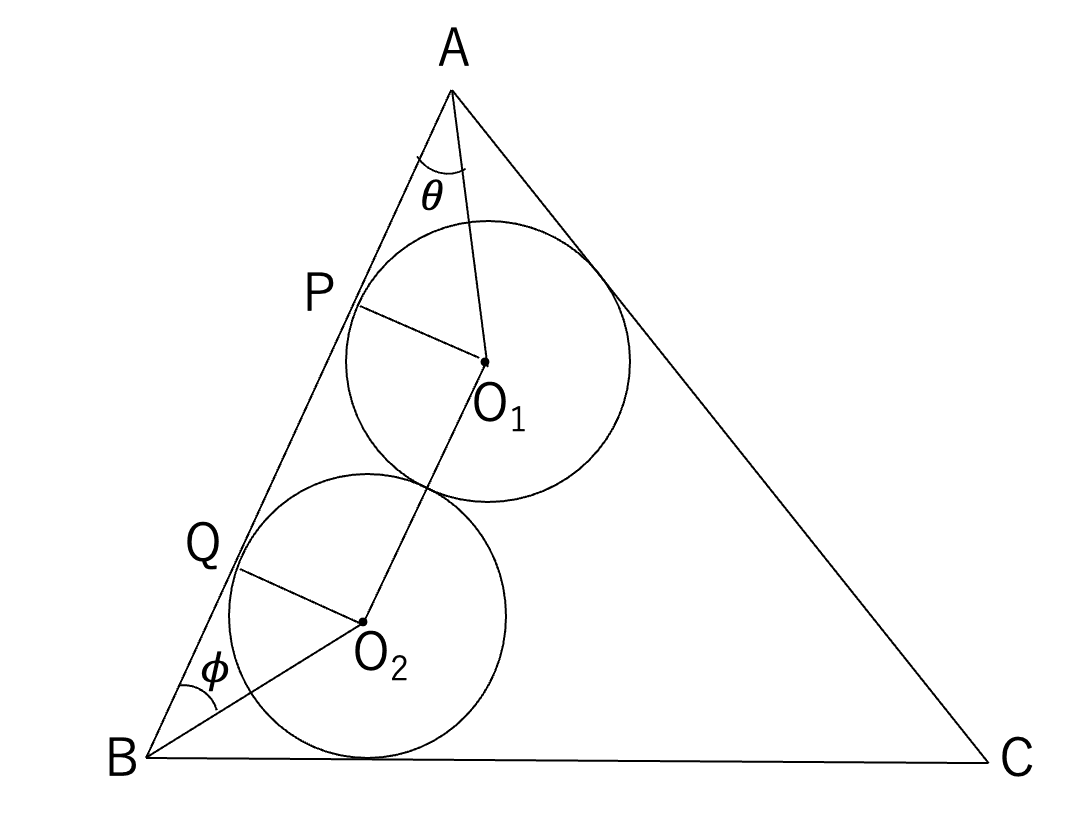
そして次はABをθとφを用いて表そうとするでしょう．cos2θとcos2φが余弦定理から求められますので，あとはこれらを用いて計算を進めていけば良さそうです．

ちなみに，ここでなぜ余弦定理を使うのかと言えば，先ほど出てきた

および

だからであり，その前の「ABをθとφを用いて表す」という方針も，AB=7を別の方法で表していますので，「ABの長さを2通りで表す」という定石を使っています．つまり

を使っているのです(図形量＝ABとしている)．

 

このように，解法体系を学べば，細かい１つ１つのステップに至るまで，一般的な理由と根拠を持って解き進められるようになります．

 

(3) B

本問は，図形の最大・最小問題です．最大・最小問題は奥が深く種類も多岐にわたり，１つの記事で一部だけ抜き出して書いても真価がわかりにくいため，本記事では割愛させていただきます．

ここでは，

「実質1変数」であり「存在条件」に帰着する

とだけ述べておきます．この意味を正確に理解したい方は，ぜひしりうすにお越しください！

 

[2] まとめ

以上が大問2でした．図形問題にも確固たる解法体系が存在するのであり，これを身につけると，場当たり的な思考をほとんど経由することなく，論理的に解法が決定できるようになるのです．

 

では，[3]の講評に入っていきたいと思います．

 

 

[3] 領域

本問は，4つの大問の中で最も取り組みやすい問題でした．領域を正確に図示し，1/6公式を使えば解くことができますので，割愛します．

受験生は本問はきちんと取れるように練習しておきましょう．

 

では，最後に[4]の講評を簡単に述べたいと思います．

 

 

[4] 微分

本問はオーソドックスな微分の問題でした．(1)(2)(4)はほとんど典型定石通りでしたし，(3)も

に注意していれば，あとはほとんど典型定石で解ける問題ですので，今回は割愛します．

ただ，典型定石とは言え，特に現役生は学習進度の関係で，数学IIIの対策が十分に実施できない場合があります．山口大医学部の数学は，数学IIIはオーソドックスな出題が多いですので，現役生は早めに対策をしておきましょう．

 

 

まとめ

以上です！かなり割愛したのにも関わらずだいぶ長文となってしまいましたが(笑)，ここまで読んでくれたみなさん，ありがとうございました．

「確固たる解法体系により，解法が『ひらめく』ものから『論理的に選ぶ』ものへと変わる」ということが，少しでも伝わっていれば嬉しいです．

 

また，本記事を読んで医学部・旧帝大専門塾しりうすに興味を持ってくれた方は，ぜひお問い合わせください．

山口市にお住まいの高校生や高卒生であれば対面授業(集団も個別も可能)が実施できるほか，山口県外など，遠方の方はオンラインも実施しております．